链表

链表是数据结构之一，其中的数据呈线性排列。在链表中，数据的添加和删除较为方便，就是访问比较耗费时间。

这就是链表的概念图。Blue、Yellow、Red 这 3 个字符串作为数据被存储于链表中。每个数据都有 1 个 “指针”，它指向下一个数据的内存地址。链表还包含下面几个特点：

数据一般分散存在内存中，无需连续
访问节点数据需要从根节点开始往下顺序访问, 时间为 O(n)
插入和删除节点只需改变指针的指向即可，时间为 O(1)

双指针技巧

双指针是链表题目中常见的技巧。常用在链表合并，快慢指针求对应位置节点，链表是否相交或成环等。

合并链表

这种题一般会利用一个虚拟链表 dummy 作为结果链表，在源链表用多个指针记录遍历位置。然后在遍历链表过程中比较大小，满足条件的加入到 dummy 中即可。

/**
 * @param {ListNode} l1
 * @param {ListNode} l2
 * @return {ListNode}
 */
var mergeTwoLists = function(l1, l2) {
    let dummy = new ListNode(), p = dummy

    while(l1 !== null && l2 !== null) {
        if(l1.val > l2.val) {
            p.next = l2
            l2 = l2.next
        } else {
            p.next = l1
            l1 = l1.next
        }
        p = p.next
    }
    p.next = l1 === null ? l2 : l1
    return dummy.next
};

👉 lc-21. 合并两个有序链表

💡 思路

新建一个空链表 dummy，while 循环判断两链表当前节点大小，较小的节点接到 dummy 末尾

/**
 * Definition for singly-linked list.
 * function ListNode(val, next) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.next = (next===undefined ? null : next)
 * }
 */
/**
 * @param {ListNode} l1
 * @param {ListNode} l2
 * @return {ListNode}
 */
var mergeTwoLists = function(l1, l2) {
    let dummy = new ListNode(), p = dummy

    while(l1 !== null && l2 !== null) {
        if(l1.val > l2.val) {
            p.next = l2
            l2 = l2.next
        } else {
            p.next = l1
            l1 = l1.next
        }
        p = p.next
    }
    p.next = l1 === null ? l2 : l1
    return dummy.next
};

👉 lc-86. 分隔链表

💡 思路

新建两个虚拟链表d1, d2，遍历链表，把小于x的存在的d1，大于等于的存在d2，最后合并两个链表。

/**
 * @param {ListNode} head
 * @param {number} x
 * @return {ListNode}
 */
var partition = function(head, x) {
    const d1 = new ListNode()
    const d2 = new ListNode()
    let p1 = d1, p2 = d2

    while(head) {
        if(head.val < x) {
            p1.next = head
            p1 = p1.next
        } else {
            p2.next = head
            p2 = p2.next
        }
        // 需要断开原链表
        const temp = head.next
        head.next = null
        head = temp
    }

    if(d1.next === null) return d2.next

    p1.next = d2.next
    return d1.next
};

👉 lc-23. 合并K个升序链表

💡 思路

这道题有两种思路，一种是分治思想，一种是采用优先队列(最小堆)。

分治：对k个链表数组进行递归切分，分到只有两个的时候进行合并返回
最小堆：把k个链表节点维护一个最小堆，每次从堆中拿出一个最小节点接入到结果链表中，时间为 O(nlogk)

/**
 * @param {ListNode[]} lists
 * @return {ListNode}
 */
var mergeTwoLists = function(l1, l2) {
    let dummy = new ListNode(), p = dummy

    while(l1 !== null && l2 !== null) {
        if(l1.val > l2.val) {
            p.next = l2
            l2 = l2.next
        } else {
            p.next = l1
            l1 = l1.next
        }
        p = p.next
    }
    p.next = l1 === null ? l2 : l1
    return dummy.next
};

/**
 * @param {ListNode[]} lists
 * @return {ListNode}
 */
var mergeKLists = function(lists) {
    let len = lists.length
    if(len == 0) return null

    let merge = (l, r) => {
        if(l == r) return lists[l]
        let mid = (l + r) >> 1
        let ll = merge(l, mid)
        let rr = merge(mid + 1, r)
        return mergeTwoLists(ll, rr)
    }
    return merge(0, len - 1)
};

TIP

对于在一定数据集中频繁的拿出最小值或者最大值，可以考虑用 堆(Heap) 这种数据结构的解决。

倒数第 K 个节点

对于单链表的第 k 个节点很简单，只要遍历一遍即可。但是对于倒数第 k 个节点，利用反向思维也就是求正向的第 n - k + 1 个节点，所以可以先遍历一遍链表求出 n，然后在从 head 节点开始走 n - k 步即可。虽然这种方法可以解决问题，但是实现并不优雅，炫酷的应该使用快慢指针的思想。如下：

主要步骤就是让快指针 fast 先走 k 步，可知再走 n - k 步就会到达表尾 null。这个时候让慢指针 slow 从头节点开始和 fast 一起出发，等 fast 等于null的时候，这个时候 slow 也刚好走了 n - k 步，也是正向的 n - k + 1 个节点，即是倒数第 k 个节点。

/**
 * 找出倒数的第k个节点
 * @param {ListNode} head 
 * @param {number} k 
 */
var findFromEnd = function(head, k) {
    let fast = slow = head
    let index = 0
    while(fast) {
        index++
        fast = fast.next   // 快指针先走k步
        if(index > k) {
            slow = slow.next
        }
    }
    return slow
}

👉 lc-19. 删除链表的倒数第 N 个结点

💡 思路

删除倒数第n个节点，可以找出倒数第n + 1节点进行next指针修改即可。注意，为了防止只有一个节点的情况，可以利用虚拟节点dummy技巧。代码如下：

/**
 * @param {ListNode} head
 * @param {number} n
 * @return {ListNode}
 */
var removeNthFromEnd = function(head, n) {
    let dummy = new ListNode(-1)
    dummy.next = head
    let node = findFromEnd(dummy, n + 1)  // 找出倒数的n+1节点
    node.next = node.next.next
    return dummy.next
};

/**
 * 找出倒数的第k个节点
 * @param {ListNode} head 
 * @param {number} k 
 */
var findFromEnd = function(head, k) {
    let fast = slow = head
    let index = 0
    while(fast) {
        index++
        fast = fast.next   // 快指针先走k步
        if(index > k) {
            slow = slow.next
        }
    }
    return slow
}

👉 lc-876. 链表的中间结点

💡 思路

正常的思路是走一遍链表求出节点个数n，然后中间节点就是第 n / 2 + 1 个节点。我们可以利用更加有技巧的方式，让快指针fast 每次走2步，慢指针 slow 每次只走一步，等fast到达末尾时，slow就是所求的中间节点。

/**
 * @param {ListNode} head
 * @return {ListNode}
 */
var middleNode = function(head) {
    let fast = slow = head
    while(fast && fast.next) {
        slow = slow.next
        fast = fast.next.next
    }
    return slow
};

环形链表

判断一个链表是否成环也可以利用快慢指针，让快指针 fast 走两步，慢指针 slow 走一步。如果 slow 和 fast 相遇，证明链表成环。否则没有。

/**
 * @param {ListNode} head
 * @return {boolean}
 */
var hasCycle = function(head) {
    if(!head || !head.next) return false
    let fast = slow = head
    while(fast && fast.next) {
        slow = slow.next
        fast = fast.next.next
        if(fast === slow) return true
    }
    return false
};

进阶要求出入环节点的话，可以在相遇点让 slow = head，然后快慢指针同时前进一步，下次相遇点即是入环节点。如下:

👉 lc-142. 环形链表 II

💡 思路

/**
 * @param {ListNode} head
 * @return {ListNode}
 */
var detectCycle = function(head) {
    if(!head || !head.next) return null
    let fast = slow = head
    while(fast && fast.next) {
        slow = slow.next
        fast = fast.next.next
        if(fast === slow) break
    }

    if(!fast || !fast.next) return null
    slow = head
    while(fast !== slow) {
        slow = slow.next
        fast = fast.next
    }

    return fast
};

相交链表

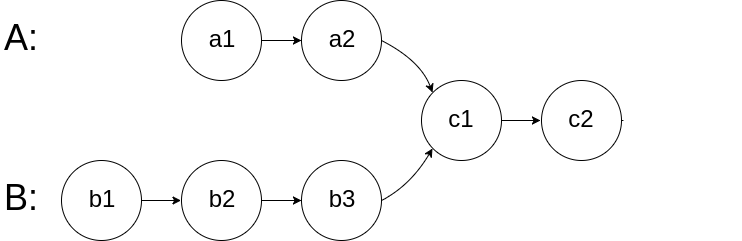
判断两个链表A， B是否相交，可以让p1遍历完A链表后遍历B链表，让p2遍历完B后去遍历A链表。如果遍历过程中存在两个节点相等，则为相交节点。

👉 lc-160. 相交链表

💡 思路

var getIntersectionNode = function(headA, headB) {
    let p1 = headA, p2 = headB
    while(p1 !== p2) {
        if(p1 === null) p1 = headB
        else p1 = p1.next

        if(p2 === null) p2 = headA
        else p2 = p2.next
    }

    return p1
};

反转链表

反转链表算法一般考察的是对递归函数的理解，包括反转整个链表，反转前K个节点以及反转某一部分节点。

反转整个链表

反转整个链表可以用迭代的方式实现，主要是多个指针的迭代指向运算：

var reverseList = function(head) {
    let curNode = null;
    let newHead = head;
    while(head && head.next) {
        curNode = head.next
        head.next = curNode.next
        curNode.next = newHead
        newHead = curNode
    }
    return newHead
};

然而，递归的方式则更加优雅。我们可以把 reverseList 理解为对 head 为头节点的链表进行反转并返回新的头节点，所以很容易通过递归函数方式写出：

var reverseList = function(head) {
    if(!head || !head.next) return head
    let last = reverseList(head.next)
    head.next.next = head
    head.next = null
    return last
};

提醒

写递归首先要明确递归函数的定义，然后确定好边界，不要试图在函数体用头脑跳进递归 😭

反转前N个节点

定义一个递归函数 reverseN(head, n) 表示反转 head 为头节点的链表的前 n 个节点，并且返回新的节点：

代码实现：

let next = null
const reverseN = function(head, n) {
    if(n === 1) {
        next = head.next
        return head
    }
    let last = reverseN(head.next, n - 1)
    head.next.next = head
    head.next = next
    return last
}

不同与反转整个链表的是，头节点 head 应该指向后驱节点 next， 即第 n+1 个节点，在 n = 1 时进行记录。

反转一部分节点

所以到这里，反转一部分链接节点的问题也可以迎刃而解。加入反转的是 [m, n] 这部分的节点，如果下面两种情况：

当 m=1 时，问题就转化成反转前 n 个节点的问题
当 m 不等于 1时候，就利用递归的思想，反转 head 链表 [m, n]，相当于 head 拼接以 head.next 为起始节点反转 [m-1, n-1] 部分节点返回的链表.

var reverseBetween = function(head, m, n) {
    if(m === 1) return reverseN(head, n)
    head.next = reverseBetween(head.next, m - 1, n - 1)
    return head
};

👉 lc-92. 反转链表 II

回文链表

不像回文字符串的判断，可以利用头尾指针往中心遍历比较，单链表只能从头部开始遍历。所以判断回文链表，有下面两种思路：

反转链表存到一个新的链表中，然后遍历两个链表进行判断
类似二叉树的后序遍历，可以对单链表进行后续遍历，如下：
js
```
function traverse(head) {
  // 前序代码
  traverse(head.next)
  // 后序代码
}
```
后序遍历单链表其实是利用栈存储遍历函数，从而可以反向访问链表节点，所以后序方式实现判断回文链表如下：
js
```
let left = head
function traverse(head) {
  if(head === null) return true
  let res = traverse(head.next)
  // 后序代码
  res = res && (left.val === head.val)
  left = left.next
  return res
}
```
这种递归的方式由于利用了栈来暂存数据，所以时间和空间复杂度都为 O(n)。如果利用 O(1) 的空间负责度如何实现？

👉 lc-234. 回文链表

💡 思路

O(1) 的空间负责度的实现思路如下:

利用快慢指针找出链表的中点 slow
反转 slow 开始到末尾的链表，获得新的链表 right
然后分别从 head 和 right 开始遍历比较

var reverse = function(head) {
    let pre = null, cur = next = head
    while(cur !== null) {
        next = cur.next
        cur.next = pre
        pre = cur
        cur = next
    }
    return pre
}

/**
 * @param {ListNode} head
 * @return {boolean}
 */
var isPalindrome = function(head) {
    let fast = slow = head
    while(fast && fast.next) {
        slow = slow.next
        fast = fast.next.next
    }

    if(fast) slow = slow.next

    let right = reverse(slow), left = head
    while(right) {
        if(right.val !== left.val) return false
        right = right.next
        left = left.next
    }
    return true
};

参考

labuladong 手把手刷链表算法

链表 #

双指针技巧 #

合并链表 #

倒数第 K 个节点 #

环形链表 #

相交链表 #

反转链表 #

反转整个链表 #

反转前N个节点 #

反转一部分节点 #

回文链表 #

参考 #

链表

双指针技巧

合并链表

倒数第 K 个节点

环形链表

相交链表

反转链表

反转整个链表

反转前N个节点

反转一部分节点

回文链表

参考